
静岡大学2022大問3
(1)の考え方を確認してみよう!
まずは可能な範囲で図形を描いてみる。そのあと比や辺の長さを書いてみてください
(例として書いてみると以下のようになります)
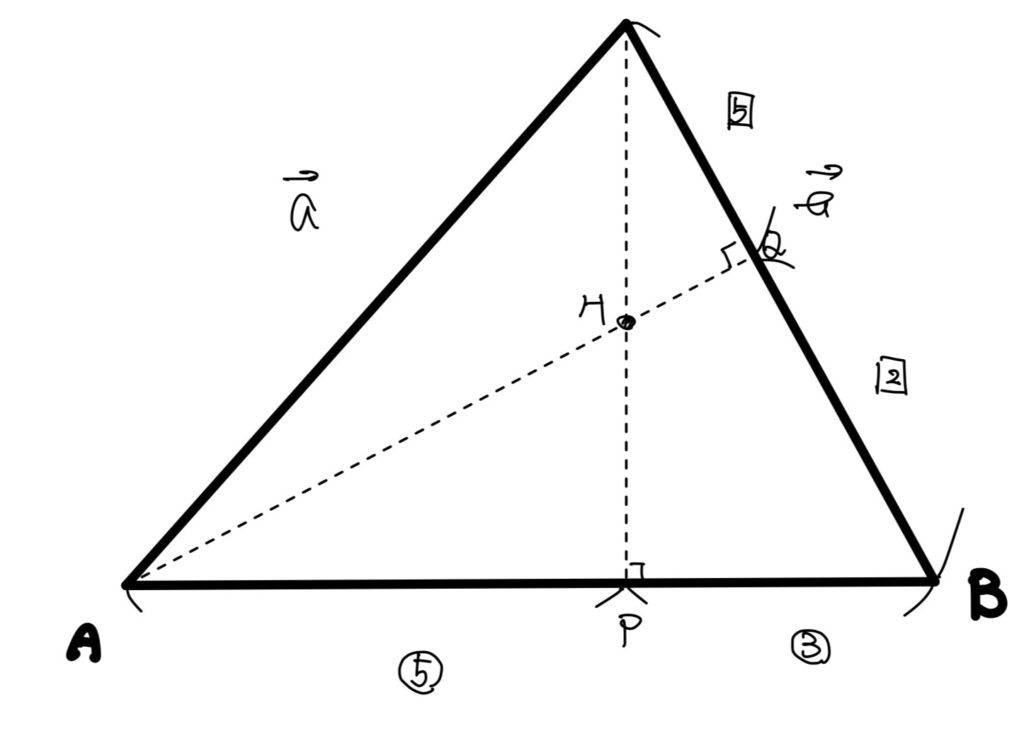
次に\(\overrightarrow{OH}\)を求めていきたいところですが、単純な内分のベクトルの公式一発では求めることは出来ません。HはOPとAQの交点なので、まずは\(\overrightarrow{OP}\)と\(\overrightarrow{AQ}\)を求めていきたいと思います。
ここで内分のベクトルの公式を一度確認しておきましょう。
線分AB上でm:nに内分する点をPとすると
\(\overrightarrow{OP}=\displaystyle\frac{n\overrightarrow{OA}+m\overrightarrow{OB}}{m+n}\)と書くことができます。
では、まず\(\overrightarrow{OP}\)を求めてみましょう
\(\overrightarrow{OP}=\displaystyle\frac{3\vec{a}+5\vec{b}}{8}\)
\(\overrightarrow{OP}=\displaystyle\frac{3}{8}\vec{a}+\frac{5}{8}\vec{b}\)となります。
次に\(\overrightarrow{AQ}\)を確認してみましょう
\(\overrightarrow{AQ}=\overrightarrow{OQ}-\overrightarrow{OA}\)となり\(\overrightarrow{OQ}\)は条件から\(\overrightarrow{OQ}=\displaystyle\frac{5}{7}\vec{b}\)なので
\(\overrightarrow{AQ}=\displaystyle\frac{5}{7}\vec{b}-\vec{a}\)となります。
ここまでで(1)を解くための材料そろったので、\(\overrightarrow{OH}\)を求めていきましょう
Hは線分OP、線分AQ上にあるので\(\overrightarrow{OH}\)は2通りで書くことができます。
\(\overrightarrow{OH}=x\overrightarrow{OP}=x(\displaystyle\frac{3}{8}\vec{a}+\frac{5}{8}\vec{b})\tag{ア}\)
(0\(\leq\)\(x\)\(\leq\)1)
\(\begin{align}\overrightarrow{AH}&=y\overrightarrow{AQ}\\\overrightarrow{OH}-\overrightarrow{OA}&=y(\displaystyle\frac{5}{7}\vec{b}-\vec{a})\\\overrightarrow{OH}&=\displaystyle\frac{5}{7}y\vec{b}+(1-y)\vec{a}\tag{イ}\end{align}\)
0\(\leq\)\(y\)\(\leq\)1
どちらの\(\overrightarrow{OH}\)も同じベクトルを表しています。
ここで\(\vec{a}\)と\(\vec{b}\)は三角形を作っているため、平行ではないので一次独立です。つまり係数比較ができます。
なので(ア)(イ)より\(\vec{a}\)と\(\vec{b}\)の係数比較をしてみましょう!
\(\left\{\array{\displaystyle\frac{3}{8}x&=(1-y)\\\displaystyle\frac{5}{8}x&=\displaystyle\frac{5}{7}y}\right.\)
すなわち\(x=\displaystyle\frac{4}{5}\),\(y=\displaystyle\frac{7}{10}\)ということが分かります。
(ア)の式に\(x\)を代入してみましょう!すると
\(\begin{align}\overrightarrow{OH}&=\displaystyle\frac{4}{5}\overrightarrow{OP}\\\overrightarrow{OH}&=\displaystyle\frac{3}{10}\vec{a}+\frac{1}{2}\vec{b}\end{align}\)
となり、\(\overrightarrow{OH}\)を求めることができました!