
(1)まずは\( \overrightarrow{PR} \)を\( \overrightarrow{AB} \)、\( \overrightarrow{AC} \)、\( \overrightarrow{AD} \)のような簡単なベクトルで表してみる。
\( \overrightarrow{PR} \)=\( \overrightarrow{AR} \)ー\( \overrightarrow{AP} \)=\(\displaystyle\frac{1}{2}\)(\( \overrightarrow{AC} \)+\( \overrightarrow{AD} \))-\(\displaystyle\frac{1}{2}\)\( \overrightarrow{AB} \)
\(|\overrightarrow{PR}|^{2}=\displaystyle\frac{1}{2} (|\overrightarrow{AC} |^2+|\overrightarrow{AD} |^2+|\overrightarrow{AB} |^2+2\overrightarrow{AC}\cdot\overrightarrow{AD}-2\overrightarrow{AB}\cdot\overrightarrow{AC}-2\overrightarrow{AB}\cdot\overrightarrow{AD})\)
ここで四角錐ABCDが正四角錐であることに着目してみよう。
全ての面の三角形が正三角形であるから\(\overrightarrow{AB}\cdot\overrightarrow{AC}=\overrightarrow{AD}\cdot\overrightarrow{AB}=\overrightarrow{AC}\cdot\overrightarrow{AD}=2\)であることがわかる。
よって
\(|\overrightarrow{PR}|^{2}=2\)
(2)
三角形SBRについて余弦定理が使えそう!
余弦定理を使うために必要な情報を集めていこ〜

必要な情報は\(|\overrightarrow{AC}|=1\)
また、\(\overrightarrow{BS}=\overrightarrow{BR}=\sqrt{3}\)である。
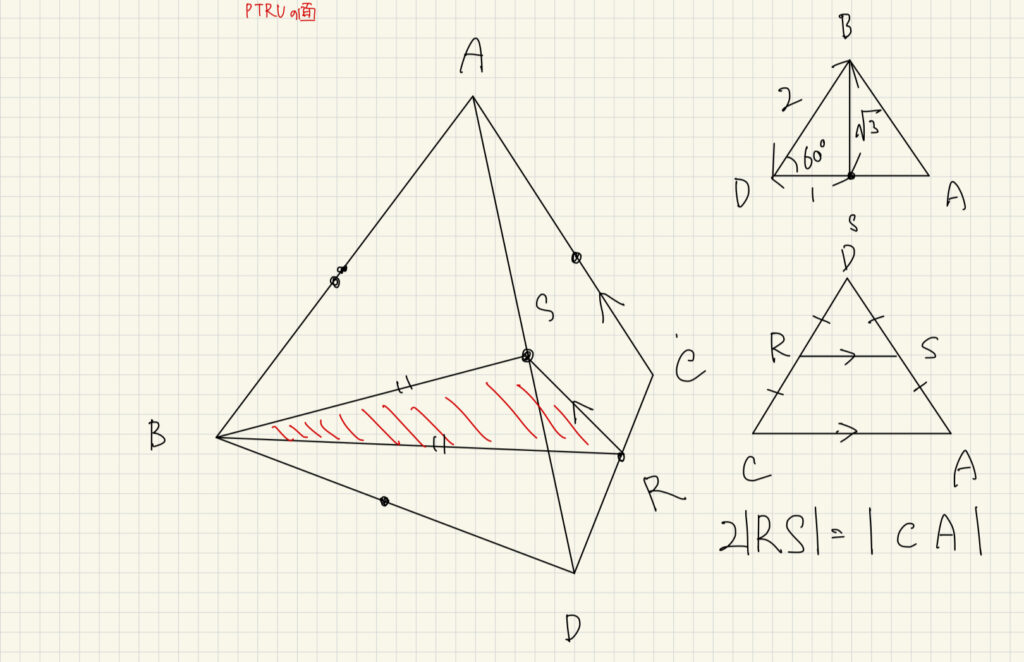
この二つの要素を用いて、\({1}^{2}=\sqrt{3}^{2}+\sqrt{3}^{2}-2 \cdot \sqrt{3}^2cos\angle SBR\)
\(5=6cos\angle SBR\)
\(cos\angle SBR=\displaystyle\frac{5}{6}\)
(3)
\( |\overrightarrow{SQ}| = |\overrightarrow{PR}|=\sqrt{2}\)
よって求める高さ\(\displaystyle\frac{\sqrt{2}}{2}\)
また、PURTは一辺の長さが1の正方形であるので、
求める面積Vは
\(V=\displaystyle\frac{1}{3}\cdot\displaystyle\frac{\sqrt{2}}{2}\cdot{1}=\displaystyle\frac{\sqrt{2}}{6}\)